Machine Learning笔记——多变量线性回归
本文共 1753 字,大约阅读时间需要 5 分钟。
在之前的单变量线性回归问题中,我们是通过房屋的大小来作为预测房屋价格。但是我们知道了很多其他的变量,例如卧室的数量,楼层的数量,房子的年龄等。
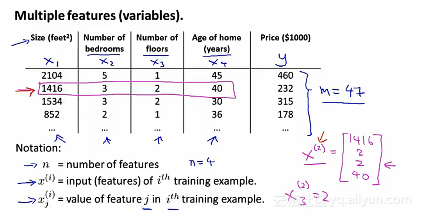 那么之前的假设函数就会不再之前的函数表达式,取而代之的是:
那么之前的假设函数就会不再之前的函数表达式,取而代之的是: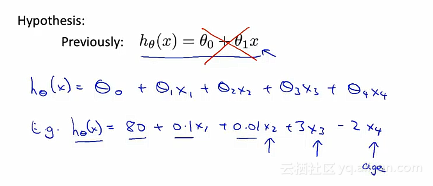 下面是重新该写后的假设函数的形式:
下面是重新该写后的假设函数的形式: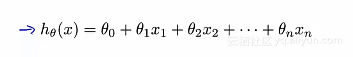 为了简化方便,涉及初始的x_0=1,
为了简化方便,涉及初始的x_0=1,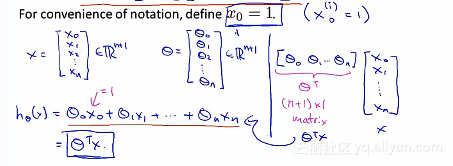 以上就是多元线性回归。多元——使用多个特征值或者是变量来预测Y的值。
以上就是多元线性回归。多元——使用多个特征值或者是变量来预测Y的值。 使用梯度下降法来处理多元线性回归问题
 执行偏导数之后如下:
执行偏导数之后如下: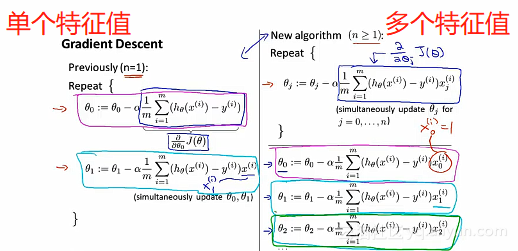 梯度下降法的应用实例——特征缩放的方法特征缩放前后,相对应的代价函数的图形也会随之不同。
梯度下降法的应用实例——特征缩放的方法特征缩放前后,相对应的代价函数的图形也会随之不同。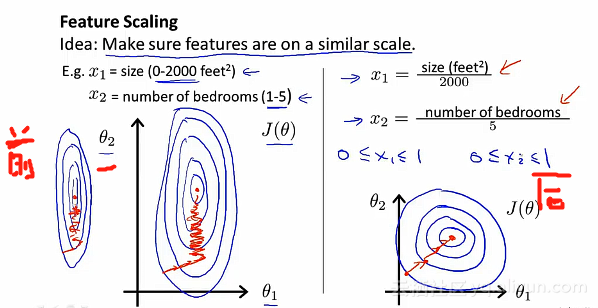 一般地,当我们执行特征缩放的时候,通常的目的是:将特征的取值约束到-1到+1的范围内。特征x_0总是等于1,也总是在此范围之内,但对于其他的特征而言,可以通过其他的分数使得它处于同一范围内,特征的值要控制在非常小的范围内。但是不能太小,也不能太大。
一般地,当我们执行特征缩放的时候,通常的目的是:将特征的取值约束到-1到+1的范围内。特征x_0总是等于1,也总是在此范围之内,但对于其他的特征而言,可以通过其他的分数使得它处于同一范围内,特征的值要控制在非常小的范围内。但是不能太小,也不能太大。 不用过于担心特征是否在完全相同的范围或者是区间内,但是只要它们之间足够接近的话,梯度下降法就会正常地运行。
不用过于担心特征是否在完全相同的范围或者是区间内,但是只要它们之间足够接近的话,梯度下降法就会正常地运行。 除了将特征除以最大值以外,在特征缩放中,会使用特征均一化的操作。

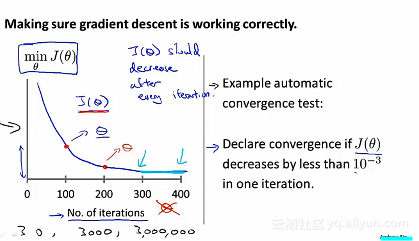 一般来说,我们可以从图形中直接可以看得出算法有没有正常地运行。例如:α过大,就会出现以下的图形:
一般来说,我们可以从图形中直接可以看得出算法有没有正常地运行。例如:α过大,就会出现以下的图形: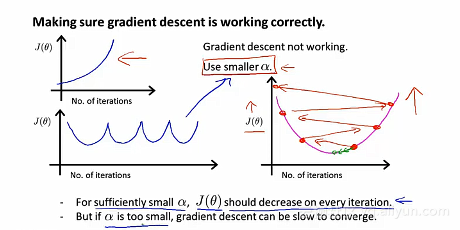 总结:如果α太小的话,就会遇到收敛速度很慢的问题,如果α太大的话,代价函数T(θ)可能不会在每次迭代都下降。甚至可能会不收敛。也会有一些情况,就是如果学习率α过大,也有可能会出现收敛缓慢,但是代价函数T(θ)并不会在每次迭代之后都下降。但是通常情况下,通常绘制T(θ)随迭代步数变化的曲线。
总结:如果α太小的话,就会遇到收敛速度很慢的问题,如果α太大的话,代价函数T(θ)可能不会在每次迭代都下降。甚至可能会不收敛。也会有一些情况,就是如果学习率α过大,也有可能会出现收敛缓慢,但是代价函数T(θ)并不会在每次迭代之后都下降。但是通常情况下,通常绘制T(θ)随迭代步数变化的曲线。 继续拿预测房价为例,除了之前的特征之外,还有其他新的特征值
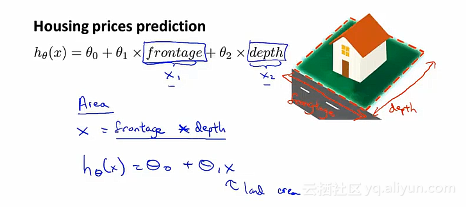
多项式回归的问题
例如:我们有如下图所示预测房子的价格的数据集,可能会有多个不同的模型用于拟合。选择之一就是二次模型,因为直线似乎并不能很好地去拟合这些数据。然而二次函数最终会下降,为了能够拟合数据集的变化,会继续使用三次方的函数,这样子就不会下降。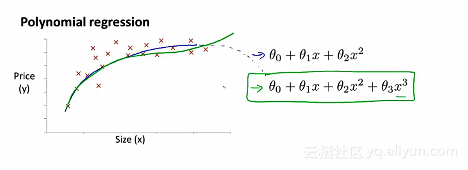 对于这样子的多元线性回归,做一下简单的修改来实现:
对于这样子的多元线性回归,做一下简单的修改来实现: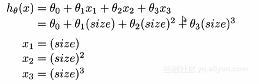 但是除了三次函数的拟合之外,采用二次函数,我们不希望说因为房子的面积的增加而导致房子的价格还下降。所以就可以使用
但是除了三次函数的拟合之外,采用二次函数,我们不希望说因为房子的面积的增加而导致房子的价格还下降。所以就可以使用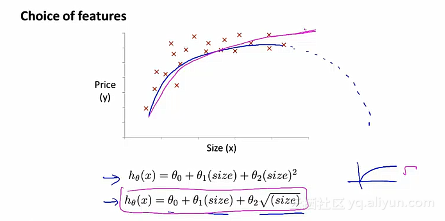 由于根式的图像是上升的,最后趋于平缓状态,也是可以拟合所给的数据集。
由于根式的图像是上升的,最后趋于平缓状态,也是可以拟合所给的数据集。 正规方程
对于某些线性回归问题,会给我们更好的方式去得到未知参数θ的最优解。在之前优质使用的方法——梯度下降法中,为了得到最小化代价函数T(θ),会使用迭代算法。通过梯度下降的多次迭代来收敛到全局最小值。实例: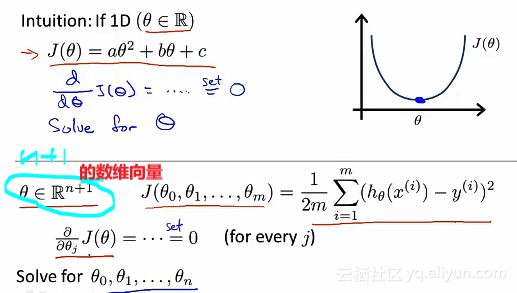 例如:假设我们有四个训练样本,这四个训练样本就是所有的数据。我们所要做的是在数据集中,加入一列来对应额外的特征变量x_0,取值永远都是1。接下来就是构建一个矩阵X(m*(n+1)维矩阵),矩阵X包括了训练样本中的所有数据,也构建一个向量y(m维向量)。其中m是训练样本数量,n和n+1是特征变量数
例如:假设我们有四个训练样本,这四个训练样本就是所有的数据。我们所要做的是在数据集中,加入一列来对应额外的特征变量x_0,取值永远都是1。接下来就是构建一个矩阵X(m*(n+1)维矩阵),矩阵X包括了训练样本中的所有数据,也构建一个向量y(m维向量)。其中m是训练样本数量,n和n+1是特征变量数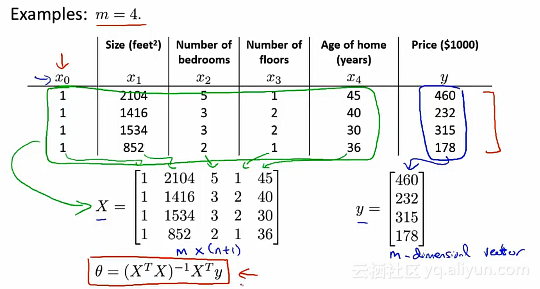 在一般情况下,假设我们有m个训练样本。其中的X称为设计矩阵(designed Matrix)
在一般情况下,假设我们有m个训练样本。其中的X称为设计矩阵(designed Matrix)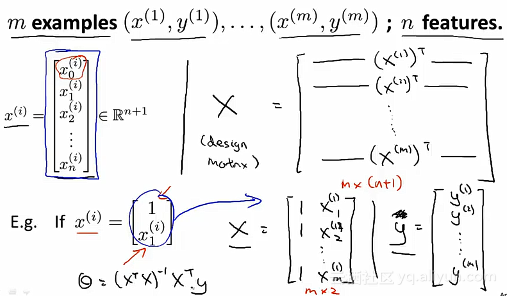 为了能够明白下列式子,作了具体的说明:
为了能够明白下列式子,作了具体的说明: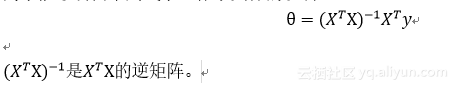 在Octave或者是MATLAB中,具体的实现方式如下:Pinv(X’X)X’*y
在Octave或者是MATLAB中,具体的实现方式如下:Pinv(X’X)X’*y 使用了正规方程,那我们直接不用特征缩放的方法。
至于什么时候正规方程和特征缩放呢?可以根据以下优缺点来判断:
假设我们有m个训练样本,n个特征变量
 使用octave绘制正余弦曲线图:
使用octave绘制正余弦曲线图: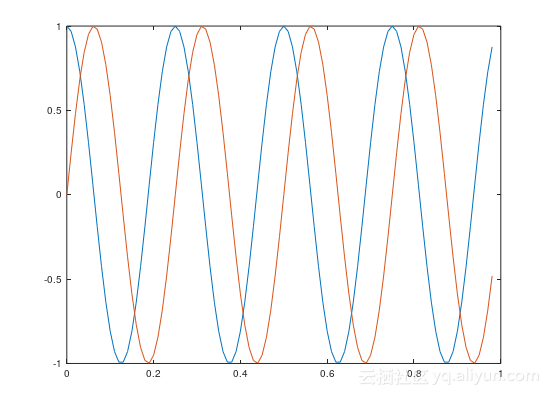 使用octave的示例代码如下:
使用octave的示例代码如下: t=[0:0.01:0.98];y1=cos(2*pi*4*t);plot(t,y1)y2=sin(2*pi*4*t);plot(t,y2)
再次绘制了正切函数之后的图像如图所示:
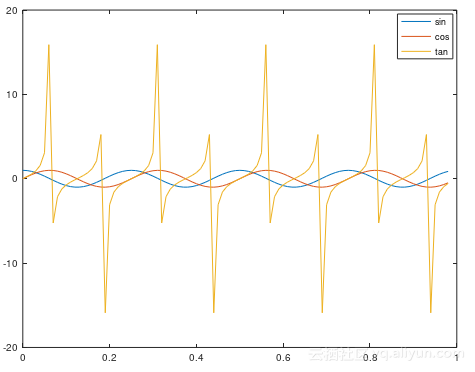
例如:使用magic函数
A=magic(5)imagesc(A)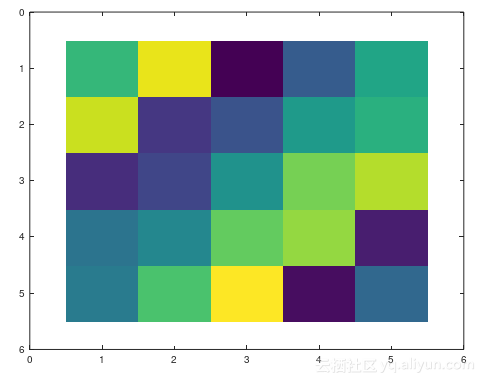
使用octave程序写控制语句
例如for i=1 :10 ;v(i)=2^i ;end ;indices=1 :10所以for i=indices;
Reference:
吴恩达 机器学习课程
转载地址:http://jkfna.baihongyu.com/
你可能感兴趣的文章
Python3.4 12306 2015年3月验证码识别
查看>>
从Handler.post(Runnable r)再一次梳理Android的消息机制(以及handler的内存泄露)
查看>>
windows查看端口占用
查看>>
Yii用ajax实现无刷新检索更新CListView数据
查看>>
JDBC的事务
查看>>
Io流的概述
查看>>
App 卸载记录
查看>>
JavaScript变量和作用域
查看>>
开源SIP服务器加密软件NethidPro升级
查看>>
百度页面分享插件源代码
查看>>
《别做正常的傻瓜》的一些读书心得
查看>>
作业:实现简单的shell sed替换功能和修改haproxy配置文件
查看>>
spring配置多数据源问题
查看>>
Altium 拼板方法以及 注意的 地方
查看>>
简明Linux命令行笔记:tail
查看>>
PMP考试的过与只是
查看>>
java 监控 收集资料3(收集中)
查看>>
实例演示如何使用AgileEAS.NET SOA平台工作流进行业务流程自定义
查看>>
Spring Cloud Alibaba迁移指南(二):零代码替换 Eureka
查看>>
聊聊BOM的那些事
查看>>